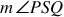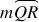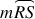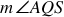William W. answered • 04/18/19
Experienced Tutor and Retired Engineer
Since m∠PAQ = 130° the measure of arc PQ = 130° (measure of minor arc equals the measure of the associated central angle). If the measure of arc PQ = 130°, then the measure of ∠PSQ = 65° (measure of an inscribed angle is half the measure of the subtended arc)
Since m∠PAQ = 130° the measure of ∠QAR = 50° (because PAR is a straight angle). If m∠QAR = 50°, then the measure of arc QR = 50° (measure of minor arc equals the measure of the associated central angle).
Because ∠SPR = 35°, the measure of arc RS = 70° (measure of an inscribed angle is half the measure of the subtended arc).
Because he measure of arc RS = 70°, the measure of arc PS = 110° (half a circle is 180°). Because the measure of arc PS = 110° and the measure of arc QR = 50°, the m∠B = 80° (add angles and divide by 2) so m∠PBQ = 100° so m∠AQS = 30° (triangle ABQ has 180°)
As mentioned above arc PS = 110°


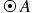 shown below has diameter
shown below has diameter 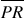 which intersects
which intersects 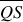 at point
at point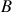 and the measurements shown. Calculate the following measures:
and the measurements shown. Calculate the following measures: