HELP WITH C-E PLEASE EXPLAIN AND GIVE ANSWER

Question

For decades, hoax artists have been going out into grain fields to make crop circles like the one shown below. Though many people believed these crop circles to be the work of aliens we now know that these designs were made by people with very simple tools and some geometric knowledge. To make each circle, one person stands stationary in a field holding a rope of a specific length, while another person holds the other end of the rope. The second person circles the first and uses a wooden plank to bend the grain stalks until all the grain in that circle lies flat against the ground. Then they both move to make other circles. The result is often very beautiful, especially when seen from the air. Along with the image below, Use your knowledge of the unit circle and radian measure of angles to answer the following questions. [Note: When the questions ask you to consider circles and their angle in relation to the main circle, the question is referring to the location of the center of each circle.]

a. Consider circles 1 through 6. If these circles are equally spaced around the main circle, and circle 1 is at 0°, what is the direction (in degrees) of each of these circles in relation to the main circle?

b. Consider circles 7 through 12. If circle 7 is at 45°, what is the radian measure of each of these circles in relation to the main circle? Explain how you know these values.

c. If the center of circle 3 is 100 feet away from the main circle, what are the coordinates of the center of circle 3 (the origin is at the center of the main circle)? Use these coordinates to prove that the distance from the centers of circle 3 and the main circle are 100 feet apart.

d. After creating the design, the designers want to inspect their work. They start at 0° and walk all the way around the design almost two times and stop at circle 12. How many radians did they cover during their inspection?

e. Consider circles 5 and 6. In relation to the main circles, do the center points of circles 5 and 6 have even or odd symmetry? Why?

Can you please help me solve the questions and show me your work?

Answer 1

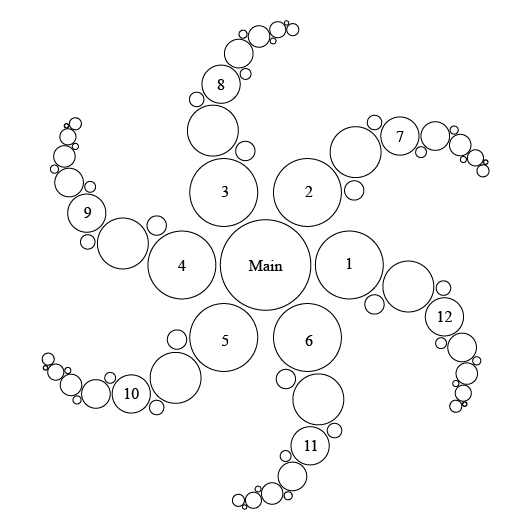
a. Consider circles 1 through 6. If these circles are equally spaced around the main circle, and circle 1 is at 0°, what is the direction (in degrees) of each of these circles in relation to the main circle?

Unit circles give us the full circumference of a circle representing 360-degrees or 2(pi) radians. If circle 1 is 0-degrees, then it also represents the position at 360-degrees. Circle 4 on the exact opposite side would be 180-degrees from which 0 --> 180 degrees form a straight line. The way to equally divy up the remaining circles 2 and 3 would be to move by 60-degrees each step. Thus, 1: 0-degrees; 2: 60-degrees; 3: 120-degrees; 4: 180-degrees; 5: 240-degrees; 6: 300-degrees; back to 1 which is 0- or 360 degrees.