
Raaya J.
asked • 12/25/21Significance level
Five measurements of the tar content of a certain kind of cigarette yielded 14.5, 14.2, 14.4, 14.3 and 14.6 mg/cigarette. Assuming that the data are a random sample from a normal population, show that at the 0.05 level of significance the true average tar content is more than 14.
1 Expert Answer
Step 1: Write your null hypothesis statement. The null hypothesis is that the average tar content is 14 so
H0: μ = 14.
Step 2: Write your alternate hypothesis. This is what you’re testing in the one sample t test. You think that there is a difference (that the average tar content is > 14), so:
H1: μ > 14.
Step 3: Obtain the following descriptive statistics you’ll need to calculate the test statistic.
- The sample mean(x̄). 14.375
- The population mean(μ). = 14
- The sample standard deviation(s) = .17078
- Number of observations(n) = 4
Step 4: Insert the items from above into the t score formula.
t = (14.375-14) / (.17078/(sqrt 4)
t = (14.375-14) / (.17078/(sqrt 4)
t= .375/.08539
t = 4.392 This is your observed t value.
Step 5: Find the critical t value in a t table. You need two values to find this:
- The alpha level: given as .05 or 5% in the question.
- The degrees of freedom, which is the number of items in the sample (n) minus 1: 4-1 = 3
In the t table. look up 3 degrees of freedom in the left column and .05 in the top row. The 1 tailed value is 2.353. This is your one-tailed critical t-value.
Step 6: Compare the observed t value to the critical t value. If the observed t is greater than the critical t, the test is significant at the .05 alpha level. Here we see that 4.392 > 2.353. The test is significant and the sample mean is significantly greater than 14.
The one sample t test has told us that the average tar content is greater than 14.
Still looking for help? Get the right answer, fast.
Get a free answer to a quick problem.
Most questions answered within 4 hours.
OR
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.



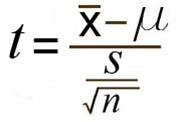



Jon S.
Do you have any specific questions about performing a single mean t-test?12/26/21