Please please help! GEOMETRY

Question

If lines p and q are parallel and angle 3 = 75^o, write the measures of all other angles. Explain your reasoning in 2 or more sentences and include your calculations.

Answer 1

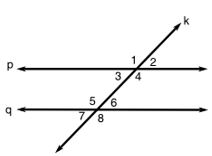
There are several angle relationships in a parallel line cut by transversals. Any two angles can either be congruent or supplementary.

The following angles are congruent:

1. Correnponding angles:
2. ⦣1≅⦣5
3. ⦣3≅⦣7
4. ⦣2≅⦣6
5. ⦣4≅⦣8
6. Alternate interior angles:
7. ⦣3≅⦣6
8. ⦣4≅⦣5
9. Alternate exterior angles:
10. ⦣1≅⦣8
11. ⦣2≅⦣7
12. Vertical angles

The following angles are supplementary (meaning their measure add up to 180^o)

1. Same side exterior
2. m⦣1 + m⦣7 = 180^o
3. m⦣2 + m⦣8 = 180^o
4. Same side interior
5. m⦣3 + m⦣5 = 180^o
6. m⦣4 + m⦣6 = 180^o
7. Linear pair

So here are the answers:

1. m⦣1 = 105^o because it is ⦣1 and ⦣3 are linear pair.
2. m⦣2 = 75^o because it is ⦣2 and ⦣3 are vertical angles.
3. m⦣3 = 75^o given.
4. m⦣4 = 105^o because ⦣4 and ⦣3 are linear pair.
5. m⦣5 = 105^o because ⦣3 and ⦣5 are same side interior angles.
6. m⦣6 = 75^o because ⦣3 and ⦣6 are alternate interior angles.
7. m⦣7 = 75^o because ⦣3 and ⦣7 are corresponding angles.
8. m⦣8 = 105^o because ⦣2 and ⦣8 are same side exterior angles.

Answer 2

The most efficient way to explain this appears to be via one of the several online resources that already exist.

For instance, this link appears to have what you need for this problem:

https://www.mathsisfun.com/geometry/parallel-lines.html