Solution for 2).
The standard process for finding inverse of a function is as follows:
A. In the stated function we change f(x) with y.
y = 4 + √(x - 2).
B. We swap x and y in the above equation.
x = 4 + √(y - 2).
C. We solve the above equation for y (steps of the solution omitted).
y = (x - 4)2 +2
Part 3. (1) Observing A above, we can say, that the domain of the function f(x) is all values of x, for which the radical has real value: x >= 2. The range of the function is all values which f(x) receives. For this function, y >=4.
(2) For the inverse, the domain and range of the inverse swap places: the domain of f becomes the range of f-1 and vise-versa.
If you have any questions, ask question.
Note: the function f(x) is one-to-one, and when we found f-1, it was not. This is why we must restrict the domain of the function f-1 to only one of the parts of the parabola.

Sava D.
07/11/20

Sava D.
07/11/20
Joshua C.
Hi Sava! That's perfect. I fully understand it now. The graph was my eureka! moment. That will definitely help me solve similar exercises in the future, thank you so much!!!07/12/20


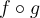
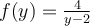
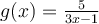
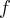
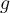
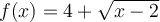
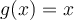




Joshua C.
Hi Sava, thank you so much for your explanation. I think that I was on the correct path but you made everything clearer to me. Really appreciate it. Would you please help me with Q3? I'm really struggling with it. Thank you so much!!07/11/20