I'm terrible with proofs, but since P is congruent to S and a quadrilateral has supplementary opposite angles, use substituion to show that P and R and/or Q and S are congruent, thus you must have four 90 degree angles.
I bet you can figure out why we can't prove it's a square!


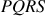 with the following information:
with the following information: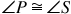
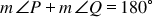
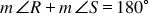
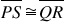
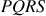 is a square?
is a square?



