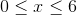Calc BC Mean Value Theorem

Question

Let f be a twice-differentiable function such that f'(2)=0. The second derivative of f is given by f''(x)=x²e^2-x -1 for

Use the Mean Value Theorem on the closed interval [2,4] to show that f'(4) cannot equal 8.5

.

Answer 1

By the Mean Value Theorem, there is at least one number, c, in the interval (2,4) such that

f"(c) = (f'(4) - f'(2)) / (4 - 2) = (f'(4) - 0) / 2

So, f'(4) / 2 = c²e^2-c - 1.

If we assume that f'(4) = 8.5, then we have c²e^2-c = 5.25.

Now, let g(x) = x²e^2-x.

g'(x) = 2xe^2-x - x²e^2-x = xe^2-x(2 - x) = 0 when x = 0 or 2.

When x < 0, g'(x) < 0. So g is decreasing.

When 0 < x < 2, g'(x) > 0. So, g is increasing.

When x > 2, g'(x) < 0, So, g is decreasing.

In particular, g is decreasing on (2,4).

So, g(2) > g(c) > g(4)

Therefore, 4e⁰ > c²e^2-c > 16e^-2 > 0.

So, 0 < c²e^2-c < 4

But, c²e^2-c = 5.25 > 4

***CONTRADICTION***

Therefore, f'(4) cannot equal 8.5.

Answer 2

According to the mean value theorem applied to the function defined by the first derivative in the interval x ∈ [2,4], there exists one value c such that

f''(c) = (f'(4) - f'(2))/(4-2). ⇒ 2f''(c) = f'(4)

Now, one can show that the f'' function is monotonically decreasing in the interval [2,4], such that its maximum value is when x = 2, and f(2) = 3. if we plug this back into the previous equation, one can see that the maximum value for f'(4) is 6, hence we have shown that it cannot be 8.5, QED

To show that f'' is monotonically decreasing, we compute f'''(x) = x(2-x)e^2-x. f''' is positive in the interval [0,2] only; since we are interested in the [2,4] interval, f''' is negative there, which proves f'' decreases there, so that x = 2 is an absolute maximum.