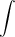Calculus Math Help

Question

Consider the following.

(a) Set up an integral for the volume a solid torus (the donut-shaped solid shown in the figure) with radii br and aR. (Let a = 3 and b = 2.)

0

 dy

(b) By interpreting the integral as an area, find the volume V of the torus.

V = 

Answer 1

Hi,

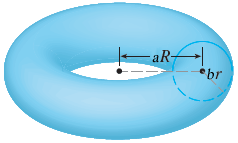
The torus is obtained by rotating the circle (x - R)^2 + y^2 = r^2 about y-axis

after solving this equation and finding x you will have:

x = R + √r²- y²= f(y) right half side

x = R - √r²- y²= g(y) left half side

so

v = Π ∫_-r^+r {[f(y)]^2 - [g(y)]^2 } dy

v = 2Π ∫₀^r [ ( R^2 + 2 R √r^2-y^2 + r^2 - y^2 ) - ( R^2 - 2 R √r^2-y^2 + r^2 - y^2)]dy

v = 2Π ∫₀^r 4R√r^2-y^2 dy= 8ΠR∫₀^r √r^2-y^2 dy

observe that the integral represents a quarter of the area of a circle with radius r, so 8ΠR∫₀^r √r^2-y^2 dy = 8 Π R * 1/4 Π r^2 = 2 Π^2r^2R

I hope it is useful,

Minoo