calculus question

Question

The rate of growth of a fish population was modeled by the equation

G(t) = 90,000e−0.6t		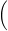1 + 5e−0.6t	2

,

where t is measured in years since 2000 and G in kilograms per year.

Write an integral to find the change in the population predicted between 2000 and 2020.

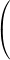		90,000e−0.6t		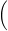1 + 5e−0.6t	2

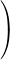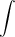 dt

Find a substitution and apply it to rewrite the integrand in the form 1

u2

 du.

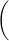
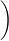		1 + 5e−12		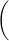1
u2
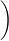	du

 

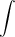If the biomass was 20,000 kg in the year 2000, what is the predicted biomass (in kg) for the year 2020? (Round your answer to the nearest whole number.)

 kg

Answer 1

Hi Taiwo,

I think I could solve this one for you, but the formatting makes it unclear what the intended equations are.