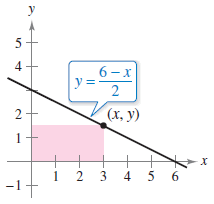please help me I'm having trouble

Question

A rectangle is bounded by the x- and y-axes and the graph of  y = (6 − x)/2 (see figure). What length (x) and width (y) should the rectangle have so that its area is a maximum?

x=

y=

Answer 1

The equation for the area of a rectangle is length * width. For us here, it would be x * y. We can substitute the equation of the line for y and get:

A = x * (6-x)/2

A = 3x - x²/2

To find the maximum of this equation, we first need to find a critical point. So we take the derivative and find the zeros:

A' = 3 - x = 0

x = 3

So we have a critical point at 3, which happens to be the maximum of the area equation. We plug this back into the line equation to get y:

y = (6 - 3)/2 = 3/2

So the rectangle with largest area has length 3 and width 3/2, with an area of 9/2.