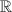Does the function satisfy the hypotheses of the Mean Value Theorem on the given interval? f(x) = 5x^2 + 5x + 4, [−1, 1]

Question

options:

1. No, f is not continuous on [−1, 1].
2. Yes, it does not matter if f is continuous or differentiable; every function satisfies the Mean Value Theorem.    
3. Yes, f is continuous on [−1, 1] and differentiable on (−1, 1) since polynomials are continuous and differentiable on .
4. No, f is continuous on [−1, 1] but not differentiable on (−1, 1).
5. There is not enough information to verify if this function satisfies the Mean Value Theorem.

If it satisfies the hypotheses, find all numbers c that satisfy the conclusion of the Mean Value Theorem. (Enter your answers as a comma-separated list. If it does not satisfy the hypotheses, enter DNE.)

c = ?

Answer 1

3 is correct. The MVT applies to any function continuous on a closed interval [a , b] (for example - 7 ≤ x ≤ 4), and differentiable on the corresponding open interval (a , b) (for example -7 < x < 4).

Polynomials such as the quadratic function f(x) given here are both continuous and differentiable over all reals.

For any function meeting the criteria listed above, the MVT guarantees at least one x-value, somewhere in between x = a and x = b, such that the instantaneous rate of change at that x-value = the average rate of change across the entire interval.

Calculating an average rate of change is simple, we just do change in y / change in x: f(-1) = 4 ; f(1) = 14

So, we have the graph going thru (-1, 4) and (1 , 14) and the avg rate of change is [14 - 4] / [1 - (-1)] = 5.

To find the c-values where the instantaneous rate of change = 5, we need to take the derivative of f(x):

f^'(x) = 10x + 5 = 5 ; x = 0.

So c = 0 is the x-value guaranteed by the MVT for f(x) on [ -1 , 1 ]

Btw, our visual understanding of the MVT is that there will be a point on the graph where the tangent line to the curve f(x) will be parallel to the secant line running thru (a , f(a)) and (b , f(b)). To understand the MVT in this way, it might be useful to use Desmos or some utility to graph f(x), the secant line thru (-1 , 5) and (1 , 14), and the tangent line to (0 , 4) (with slope = 5) all on the same set of axes.