The equation for heat loss presumably is
dT/dt = -k(T-2)
dT/(T-2) = -kt and the solution is
T = 2+Ce-kt where C and k are to be determined from the initial conditions.
You should be able to determine C and k to solve the problem completely.
T=temperature, t=time.
When t=0, T=21 and when t=1, T=16.
Plug these values pairs into the equation for T and get a pair of simultaneous equations which you can solve for k and C. This will allow you to evaluate T for any other value of t.


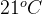 to the outdoors, where the temperature is
to the outdoors, where the temperature is 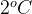 . After one minute the thermometer reads
. After one minute the thermometer reads 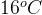 .
.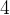 more minutes?
more minutes?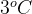 ?
?



Wonder G.
I am confused which number you are talking about...09/28/21