(Falling ladder question); A ladder 25 ft long is leaning against a wall. The base of the ladder is pulled away from wall at rate of 2ft/sec.

Question

A ladder 25 feet long is leaning against the wall of a house. The base of the ladder is pulled away from the wall at a rate of 2 feet per second.

(a) What is the velocity of the top of the ladder when the base is given below?

7 feet away from the wall

= ? ft/sec

(b) 15 feet away from the wall

 = ? ft/sec

(c) 20 feet away from the wall

 = ? ft/sec

(d) Consider the triangle formed by the side of the house, ladder, and the ground. Find the rate at which the area of the triangle is changing when the base of the ladder is 20 feet from the wall.

= ?  ft²/sec

(e) Find the rate at which the angle between the ladder and the wall of the house is changing when the base of the ladder is 20 feet from the wall.

 = ? rad/sec

I know the answers for (a, b, c) being -7/12, -3/2, and -8/3

But how do I approach questions (d) and (e)?

Thank you very much in advance for any help!

Answer 1

( d )

A = ( 1 /2 ) x y

d A / d t = ( 1 / 2) [ y {d x / d t} + x { d y / d t } ]

d A / d t = ( 1 / 2) [ ( 15) {2} + 20 { - 8 /3 } ] = - 35 / 3 ft² /sec

( e )

tan φ = x / y

( d / d t )[ tan φ ] = ( d / d t ) [ x / y ]

sec² φ (d φ / d t ) = { y d y/d t - x d y /d t } / y²

( 25 / 16 ) (d φ / d t ) = {15 ·2 − 20 · ( - 8/3 )} / 225

(d φ / d t ) = 32/ 135 rad / sec

Answer 2

d) -35/3 = change in area ft^2 per second

e) 2/15 = change in angle radians per second

2/15 rad/sec = 180/pi x 2/15 = 24/pi degrees= about

7.64 degrees per second

It might be useful to look at

a, b and c, especially c

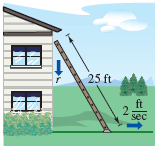
25^2 - 7^2 = 625 - 49 = 576

sqr576 = height of the ladder = 24

l^2 = h^2 + b^2 where b=7, l=25, h=24

take the derivative

2ll' = 2hh' + 2bb'

ll' = hh' + bb', l' =0 the ladder is not changing its length

0 = 24h' + 7(2)

24h' = -14

h' = -14/24 = -7/12 feet per second = change in position of the top of the ladder to the ground

change 7 to 15 and 24 becomes 20 and h=-2(15)/20 =-3/2

change b' to 20 and b becomes 15, and h =-2(20)/15=-8/3

Area of the triangle= A = half base times height = bh/2

take the derivative with b=20, h=15, b'=2, h'=-8/2

A' = (1/2)(bh' +hb') = (1/2)(20(-8/3) +15(2)) =(1/2)(-160/3 + 90/3) = (1/2)(-70/3) = -70/6 = - 35/3 ft^2/sec

Let the angle between the ladder, l, and wall, h, = B

tanB =opposite side over adjacent side = b/h

b=20, h=15, h'=-8/3, b'=2,

secB = l/h = 25/15=5/3

tanB = b/h

take the derivative

(tanB)' = (b/h)'

sec^2B(B') = (hb'-bh')/h^2 = (15(2) - (20)(-8/3))/15^2

(5/3)^2 (B') = (30 +160/3)/225 =(90/3 + 160/3)/225 = (250/3)/(225) =10/27

B' = (10/27)(9/25) = 2/15

It's easier computations with

sinB=20/25 =4/5 cosB=3/5

l'=0

the ladder doesn't change length

sinB= b/l

take the derivative

(sinB)' =(b/l)'

cosB(B') = (lb'-bl')/l^2 = (25(2) -20(0))/25 = 25(2)/25^2 = 2/25

(3/5)B' = 2/25

l'=0, the ladder doesn't change length

B' = 2/25(5/3) = 2/15

change in the angle = B' = 2/15 rad/sec = about 7.64 degrees per second

check that answer

in one second b increases from 20 to 22

sinB increases from 4/5 to 22/25

B increases from 53.13 to 61.64

61.64-53.13= 8.51 which is close to 7.64, less than 1 degree apart. B' is the instantaneous change at a point, = 7.64

8.51 is the average change over an interval of 1 second