
Isaiah W.
asked • 07/27/21Find the sum of the equation
Find the sum.
| (a) 1 |
| 3 |
| + 2 |
| 32 |
| + 22 |
| 33 |
| + 23 |
| 34 |
+ 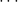 + 29 + 29
|
| 310 |
S =
| (b) 1 + 1 |
| 21/2 |
| + 1 |
| 2 |
| + 1 |
| 23/2 |
+ 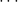
S =
1 Expert Answer
The first sequence is:
20·31 + 21·32 + 22·33 + ... + 29·310
Each term is of the form 2n-1·3n. You can write this as 2n-1·3n-1·3 = 3·6n-1
which is a standard geometric sequence. Use the summation formula for a geometric sequence to find the answer.
Sum = a·(1-rn) / (1-r)
where a = 3 and r = 6 and n = 10.
-------
The second sequence has the form:
1·2(n-1)/2
which is geometric. Use the geometric summation formula given above to find the sum when a = 1, r = 2, n = 4.
Still looking for help? Get the right answer, fast.
Get a free answer to a quick problem.
Most questions answered within 4 hours.
OR
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.






Joanie L.
Please try and repost your question without the table. Try posting each part of your question on a single line so that it's easier to read.07/27/21