The figure shows a graph of y = x4 − 2x3 − x2 + 2x.

Question

The figure shows a graph of y = x⁴ − 2x³ − x² + 2x.

Use the graph to do the following.

(a) Find the solutions of the equation x⁴ − 2x³ − x² + 2x = 0.

 (Enter your answers as a comma-separated list.)

x = 

 

(b) Find the solutions of the inequality x⁴ − 2x³ − x² + 2x ≤ 0.

 (Enter your answer using interval notation.)

 

Answer 1

Part a

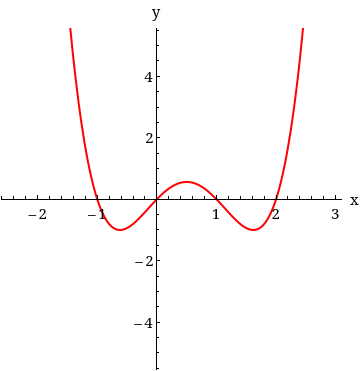
With a graph, we can find all of the solutions to the equation by looking for all of the x-intercepts. On this graph, the line of our equation crosses the x-axis at -1, again at 0,1, and 2. All of these points are our solutions.

x = -1, 0, 1, 2

Part b

When an inequality is added to the equation, we are not looking for a single value as the answer. The solution will be a range of values, not a single value. Since our equation is ≤ , we need the sections where the equation is below the x-axis. On the graph, the line drops below the x-axis at -1 and crosses into the top quadrants at 0. So, [-1,0] is our first range. We do not want to include any sections above the x-axis, which is why we stop the interval at 0. However, our line crosses the x-axis again. The line crosses the x-axis into the bottom quadrants at 1 and crosses into the top quadrants at 2. This is our second range. We write this solution as [-1, 0]U[1,2].

x = [-1, 0]U[1,2]

Answer 2

a) The solutions are the four x-values where the graph crosses the x-axis. Just read them off the graph.

b) The solutions are the two intervals where the graph is on and below the x-axis. The first one is [-1,0]. What is the second interval?