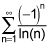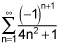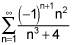Tests for Convergence (Not test questions)

Question

 

1.Use the alternating series test to determine the convergence/divergence of the series  .

	The alternating series fails.
	The series converges.
I chose this	The series is conditionally convergent.
	The summation must start with n = 0 so the alternating series test cannot be applied.

2.Which of the following series is/are convergent by the alternating series test? (4 points)

1. 
2. 
3. 

	I only
	II only
I chose this	I and II only
	I, II, and III

Please check my answer, thank you in advance!

Answer 1

Your answer to the first question is correct.

The alternating series test says that if the absolute value of the terms in the sequence converges to 0, then the series will converge. When the alternating series converges while the absolute value series diverges, this series is said to be conditionally convegent (as opposed to a series that converges absolutely). The harmonic series is such an example, as is the example in the first question, which is essentially the harmonic series, 1/n.

I don't agree with your answer for the second question, however I don't actually see a valid answer choice. 2) and 3) are both clearly convergent by the alternating series test, with 2) converging absolutely.

Regarding 1), the sequence 1/ln(n) converges at least conditionally, since lim_n→∞ 1/ln(n) = 0, but the first term in the series (as it is written) for n = 1 is -1/ln(1) which is undefined.

My best guess is that the series in 1) was meant to be written as starting at n = 2, in which case the correct answer would be I, II, and III.
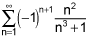