Your choice is not true (I'm sorry). While the sequence and the integral converge or diverge together (ie if one converges the other does too and vice versa), it is almost always the case that the limit of the series is not equal to the limit of the integral.
Ex. limn→∞ ∑k =1n 3-k = 1/3 + 1/9 + ... = 1/3 / 2/3 = 1/2 but limx→∞ ∫1x 3-t dt = - 1/ln3·3-x ]1∞ = 1/(3ln3)
The first answer choice is correct. The nth term test can be used to show that a series diverges, but not to show that it converges. This is true because the limit of the terms in the generating sequence = 0 is a necessary but not sufficient condition to show that a series converges.
In other words, if limn→∞ an ≠ 0, then the series diverges, but if limn→∞ an = 0, then the series may or may not converge. The most common example of this is the harmonic sequence/series, an = 1/n, in which the terms in the sequence converge to 0 ( 1 , 1/2, 1/3 , 1/4, ...) but the sum diverges (! + 1/2 + 1/3 + 1/4 + ... → ∞).


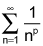 converges if p < 1 and diverges if p > 1.
converges if p < 1 and diverges if p > 1.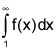 converges, then
converges, then 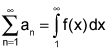 .
.


