Tom K. answered • 11/05/20
Knowledgeable and Friendly Math and Statistics Tutor
If you think about what this curve looks like (r has a maximum at θ = π/2 and the function will be symmetric about the y-axis), we should expect a slope of 0.
Note that, at θ = π/2, r = 2 sin θ, so r = 2, x = r cos θ and y = r sin θ, so (x, y) = (0, 2)
Not the most elegant solution, but let's re-express the equation in Cartesian coordinates, and it will be easy to show dy/dx at x = 0
As y = r sin θ, sin θ =y/r
Then,
r = 2 sin θ
r = 2 y/r
r2 = 2y
x2 + y2 = 2y
We could simply note that we can rewrite this equation as
x2 + y2 - 2y = 0, or, completing the square,
x2 + y2 - 2y + 1 = 1
x2 + (y - 1)2 = 1
This is a circle with center (0, 1) and radius 1, so at (0, 2), we have a horizontal tangent.
However, if we start from x2 + y2 - 2y = 0, we can use implicit differentiation to solve for the slope.
2x dx + (2y - 2) dy = 0
dy/dx = -2x/(2y - 2) = -x/(y - 1)
At (0, 2), this equals -0/(2 - 1) = 0


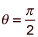 . (4 points)
. (4 points)

