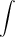Need help with Intergration of Parts Calculus

Question

Evaluate the integral.

π

4t sin 19t dt

0

Answer 1

Let u = 4t, then dv = sin(19t) dt => du = 4 dt and v = ∫sin(19t) dt = -1/19 cos(19t)

uv - ∫v du

= 4t(-1/19) cos(19t) - ∫-1/19 cos(19t) (4 dt)

= -(4/19) t cos(19t) + 4/19 ∫ cos(19t) dt

= -(4/19) t cos(19t) + 4/19(1/19) sin(19t)

= [-(4/19) π cos(19π) + 4/19(1/19) sin(19π)] - [-4/19 (0) cos(19(0)) + 4/19(1/19) sin(19(0))]

= [-(4/19) π (-1) + 4/19(1/19) (0)] - [0 + 0]

= 4π/19

Answer 2

u = 4t, du = 4dt; dv = sin19tdt, v =∫sin19tdt = -1/19cos19t.

Now ∫₀^π4tsin19dt = 4t(- 1/19cos19t)₀^π - ∫₀π(-1/19cos19t)4dt = 4π/19 + 4/19²sin19t₀^π = 4π/19