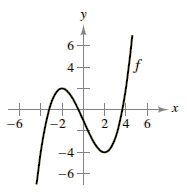which value of x is f" (x) negative?

Question

The graph of f is shown in the figure.

For which values of x is f ''(x) negative? (Enter your answer using interval notation.)

 

 

Answer 1

Note: I am assuming (0,-1/2) is an inflexion point of f(x) and that the slope of f(x) at this point is -2.

For x in the domain (-∞,-2), f '(x) is positive and decreasing. At x = -2,

f '(-2) = 0. For x in the domain (-2,0), f '(x) is negative and decreasing. At x = 0, f '(0) = -2, which is a minimum value for f '(x). For x in the domain (0,2), f '(x) is negative and increasing. At x = 2, f '(2) = 0. For x in the domain (2,∞), f '(x) is positive and increasing.

For x in the domain (-∞,0), f ''(x) is negative because f '(x) is continually decreasing in value in this domain. At x = 0, f ''(x) = 0, since this is a local minimum for f '(x). For x in the domain (0,∞), f ''(x) is positive because f '(x) is continually increasing in value in this domain.