
William W. answered • 02/22/20
Top Pre-Calc Tutor
There are two conditions the the line to be tangent to the function. 1) the function and the line must intersect. 2) the slope of the tangent line of the function must be the same as the slope of the line y = 4x + 4
For condition 1: If y = k√x and y = 4x + 4 then k√x = 4x + 4 or k = (4x + 4)/√x
For condition 2: if f(x) = k√x, we can write it as f(x) = k(x)1/2 and using the power rule, we can take the derivative so f ' (x) = 1/2k(x)-1/2 or k/(2√x) and that derivative must equal the slope of the line y = 4x + 4 (or 4) which means k/(2√x) = 4 or k = 4(2√x) or k = 8√x
So, putting conditions 1 and 2 together, k = (4x + 4)/√x and k = 8√x we can say that:
(4x + 4)/√x = 8√x
(4x + 4) = 8√x(√x)
4x + 4 = 8x
4 = 4x
x = 1
since (from condition 2) k = 8√x then k = 8√1 or k = 8


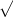 x
x


