Geometry (please help, quick)

Question

Look at the figure below:

Which triangle is similar to triangle PQR?

Triangle RQS

Triangle QTS

Triangle STQ

Triangle SPR

Answer 1

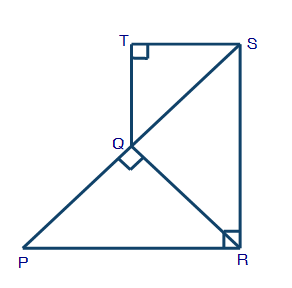
Technically all of them are similar because congruent triangles also meet the definition of similar triangles, but

triangle QTS is ONLY similar.

Update:

My original answer is not quite correct.

It is well known that in a right triangle the altitude from the right angle to the hypotenuse divides the triangle into two similar triangles which are also similar to the original triangle; this theorem provides the basis for a short proof of the Pythagorean theorem and the law of cosines.

Triangle QST is also similar since the sides are perpendicular to the sides of the original triangle.

There are NO congruent triangles in the figure.