Hi Selene!
In order to answer this question, we can break down the problem into smaller pieces to help us.
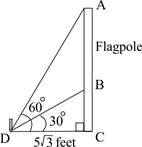
If we can find the length of AC, as well as BC, we can subtract the two values to find the length of AB.
AB = AC - BC
There are different ways to evaluate this, but suppose we wanted to use trigonometric functions to help us in this situation.
If we take a look at the larger triangle ACD first and reference its 60° angle, we will find that we know the length of the side adjacent to that angle (CD), which is equal to 5√3 ft., and we're wanting to identify the length of the side opposite (across from) this angle (AC).
The trigonometric function that compares the opposite and adjacent sides (the two legs of the right triangle) is tangent - the ratio being opposite/adjacent.
Therefore, if we take the tangent of 60°, the setup would be:
tan(60°) = AC/(5√3) -> Multiply 5√3 on both sides to get the length of the opposite side.
5√3*tan(60°) = 15
AC = 15 ft.
If we now take a look at the smaller triangle BCD and reference its 30° angle, we will find that we know the length of the side adjacent to that angle (CD) again, which is equal to 5√3 ft., and we're wanting to identify the length of the side opposite (across from) this angle (BC). This means we can use tangent again as well!
Therefore, if we take the tangent of 30°, the setup would be:
tan(30°) = AC/(5√3) -> Multiply 5√3 on both sides to get the length of the opposite side.
5√3*tan(30°) = 5
BC = 5 ft.
With the length of AB equaling AC - AB, we can take 15 - 5 and that will give us 10 ft!
What is another way? Well, notice how triangle ACD and BCD are both going to be 30°/60°/90° right triangles! This is a special right triangle, as we know the ratio between the lengths of 3 sides is 1:√3:2 (try the Pythagorean Theorem to confirm!). This can be a quicker way to determine the length of AB as we wouldn't need to utilize the trigonometric function!
If we look at triangle ACD first, we know that angle A is where the 30° is going to lie, so that means CD is the shortest side of this triangle. With the longer leg AC (across the 60°) being √3 times longer, 5√3 * √3 will get us 5*3 = 15 ft., so AC = 15 ft.
If we look at triangle BCD next, we know that angle BDC is where the 30° is going to lie, so that means BC is the shortest side of the triangle, and CD is √3 longer, so if we take 5√3 and divide by √3, we get 5, so BC = 5 ft.!
AB = AC - BC = 15 - 5 = 10 ft.
If you have any other questions, feel free to reach out and let me know!
Thanks!