Hi Selene!
In order to understand this relationship, let's first make sure we know what sine and cosine separately define.
The sine of an angle measurement is going to evaluate for us the ratio between the lengths of two sides in a right triangle, specifically the length of the side opposite the angle and the length of the hypotenuse.
So if we would like to evaluate the sin of x degrees in this instance (or sin x), we will want to locate the side opposite (or across) from this angle, which is the one with the length of 3. The hypotenuse is the longest side of a right triangle, and the length is 5.
Therefore, the sin x = length of the side opposite angle x/length of the side of the hypotenuse = 3/5.
The cosine of an angle measurement is going to evaluate for us the ratio between the lengths of two sides in a right triangle as well, specifically the length of the side adjacent (next to) to the angle and the length of the hypotenuse.
So since we're referencing angle y here, even though we have two sides that are next to angle y, we are comparing the length of one of the legs to the longest side, the hypotenuse. Therefore, the side adjacent to angle y will be using the side with length of 3.
This means cos y is the Length of the side adjacent to angle y/Length of the side of the hypotenuse = 3/5.
The answer is going to be the first answer choice as a result! The ratios of sin x and cos y are both identical.
Feel free to reach out to me if you have any additional questions or would like to schedule a session to discuss through!
Thanks!



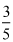 and
and 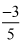 and
and 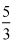 ).
).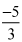 and
and 


