J.R. S. answered • 03/23/24
Ph.D. University Professor with 10+ years Tutoring Experience
CO2(g) + C(s) <==> 2CO(g)
First, let us determine in which direction the reaction will proceed. We will compare Q to Kp.
Q = (CO)2 / (CO2) = (5.31)2 / 1.35
Q = 20.9 which is much greater than Kp of 1.50. This tells us the reaction will proceed to the LEFT, or will go back to make reactant in order to attain equilibrium.
Now, we can set up the ICE table as follows:
CO2(g) + C(s) <==> 2CO(g)
1.35.........................5.31..........Initial
+x...........................-2x.............Change
1.35+x....................5.31-2x......Equilibrium
Kp = (5.31-2x)2 / 1.35-x
1.50 = (5.31-2x)2 / 1.35-x
2.03 + 1.50x = 4x2 - 21.2x + 28.2
4x2 - 22.7x + 26.2 = 0 and solve using the quadratic equation
x = 1.61 atm
(a) Equilibrium partial pressure of CO = 5.31 - 2x = 5.31 - 3.22 = 2.09 atm
(b) Equilibrium partial pressure of CO2 = 1.35 + x = 2.96 atm
Check if this is feasible by plugging these values into the Kp expression and solving for Kp:
Kp = (2.09)2 / (2.96)
Kp = 1.48 ≈ 1.50 which is the value given as the Kp.



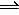 2CO(
2CO(


