solving question

Question

A ladder 25 feet long is leaning against the wall of a house. The base of the ladder is pulled away from the wall at a rate of 2 feet per second.

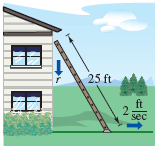
(a) What is the velocity of the top of the ladder when the base is given below?

7 feet away from the wall

 ft/sec

15 feet away from the wall

 ft/sec

20 feet away from the wall

 ft/sec

(b) Consider the triangle formed by the side of the house, ladder, and the ground. Find the rate at which the area of the triangle is changing when the base of the ladder is 20 feet from the wall.

 ft²/sec

(c) Find the rate at which the angle between the ladder and the wall of the house is changing when the base of the ladder is 20 feet from the wall.

 rad/sec

Answer 1

hypotenuse squared = sum of squares of the other sides

h^2 = b^2 + a^2

2hh' = 2bb' + 2aa'

hh' = bb' + aa' h'=0

aa' = -bb' b= 7, b' =2

a = sqr(25^2 - 7^2) = sqr(625-49) = sqr(576) = 24

a=24

a' = -7(2)/24 = -14/24 = -7/12 ft/sec = rate of change of the top of the ladder to the ground

for b=15

a' = -15(2)/24

0 = -30/24 =-3/2 ft/sec = rate of change of the top of the ladder

for b=20

a' = -20(2)/15 = -8/3 ft/sec

It's moving faster for larger base length

as the ladder base length approaches the length of the ladder

a' =-2(25/0) = -infinity

Answer 2

Let (0,y) is atop and (x, 0) bottom. Then x² + y² = 625 (1). We differentiate this equation by time:

2xdx/dt + 2ydy/dt = 0, or xdx/dt + ydydt = 0 (2); dx/dt = 2 ft/sec

(a) x = 7 ft; then from (1) 49 + y² = 625; y = 24 ft.

Now fronm (2) we have: 7·2 + 24dy/dt = 0; dy/dt = - 7/12 ft/sec (y decreasing)

x = 15 ft then from (1) y = 20 ft and 15·2 + 20dy/dt = 0; dy/dt = - 1.5 ft/sec (y decreasing)

x = 20 ft then from (1) y = 15 ft and 20·2 + 15dy/dt = 0; dy/dt = - 8/3 ft/sec (y decreasing)

(b) Area A = xy/2; dA/dt = ydx/dt/2 + xdy/dt/2 = 15·2/2 + 20(- 8/3)/2 = 15 - 80/3 = - 35/3 ft²/sec (A decreasing)

(c) tanθ = x/y; sec²θdθ/dt = (ydx/dt - xdy/dt)/y²; dθ/dt = (ydx/dt - xdy/dt)cos²θ/y² =

(15·2 - 20(- 8/3))(15/25)²/15² = 0.4 rad/sec