Maclaurin Series (Not a test question)

Question

Use the three non-zero terms of a Maclaurin series to estimate .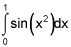

	0.3107
	0.3102
	0.3100
I chose this	0.3103

Answer 1

For the Maclaurin Series for f(x) = sin x, establish:

f(0) is sin 0 or 0;

f'(0) is cos 0 or 1;

f''(0) is -sin 0 or 0;

f'''(0) is -cos 0 or -1.

At f^(iv), one obtains -(-sin 0) or 0, so the cycle {0, 1, 0, -1} repeats forever.

Then the Maclaurin Series for sin x is generated by ∑_{(from n = 0 to ∞)}(-1)ⁿx^{(2n + 1)} ÷ (2n + 1)!,

which produces x − x³/3! + x⁵/5! − x⁷/7! + x⁹/9! − ...

Next write ∑_{(from n = 0 to ∞)}(-1)ⁿx^{(4n + 2)} ÷ (2n + 1)! (with the power expression for x doubled)

in order to gain the generator for sin (x²).

Then sin (x²) is expanded as x² − x⁶/3! + x¹⁰/5! − x¹⁴/7! + x¹⁸/9! − x²²/11! + x²⁶/13! − ...

This last is integrated term-by-term to

x³/3 − x⁷/(7•3!) + x¹¹/(11•5!) − x¹⁵/(15•7!) + x¹⁹/(19•9!) − x²³/(23•11!) + x²⁷/(27•13!) − ...

A programmable calculator with a factorial capacity of 69! will sum this last expansion with x = 1

to 0.3102683017.

This same calculator will run a Riemann-Sum program with x incremented by 0.0001 for 10000

loops to 0.3103103762.