Given:In ⊙O, OA = 15, BC = 18, and CD = 12. Find:AABCD in square units. ( PLEASE GIVE ME THE ANSWER. IVE BEEN struggling

Question

Consider the following figure.

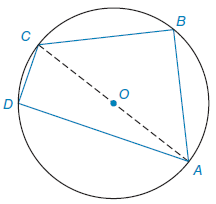A circle contains a quadrilateral with four labeled vertices, a labeled center point, and a dashed line segment.

1. Each vertex of the quadrilateral A B C D is on the circle.
2. The first side of the quadrilateral starts at vertex A, goes up and to the left, and ends at vertex B.
3. The second side of the quadrilateral starts at vertex B, goes down and to the left, and ends at vertex C.
4. The third side of the quadrilateral starts at vertex C, goes down and to the left, and ends at vertex D.
5. The fourth side of the quadrilateral starts at vertex D, goes down and to the right, and ends at vertex A.
6. The center of the circle is point O.
7. A dashed line segment starts at vertex C, goes through the center point O, and ends at vertex A.

Given:In ⊙O, OA = 15, BC = 18, and CD = 12.

Find:A_ABCD in square units

Answer 1

Two right triangles

AC = 30

BC = 18

AB² = 30² - 18² Pythagoras

CD = 12

AC = 30

AD² = 30² - 12²

ABD = (0.5)(AB)(AC)

ACD = (0.5)(AD)(AC)

ABCD = ABD + ACD

Answer 2

OA is a radius so radius = 15

OC is also a radius = 15 so AC = 30

Angle in a semicircle is 90^° so ABC is a right triangle with angle B = 90

You can use Pythagoras Theorem to find the length of BA as you know the other 2 sides

Then area of ABC = 1/2 x. length of BC x length of BA

Similarly angle D is 90 so you can find length of DA using Pythagoras Theorem

Then area of ADC = 1/2 x length of CD x length of BA

Then add the area of the two triangles together