Given:AE = 7, EB = 4 DC = 16. Find:DE and EC (Assume DE > EC.)

Question

Consider the following theorem.

If two chords intersect within a circle, then the product of the lengths of the segments (parts) of one chord is equal to the product of the lengths of the segments of the other chord.

O is the center of the circle.

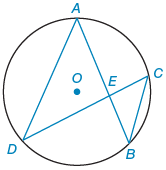A circle contains six labeled points and four line segments.

1. The center of the circle is point O.
2. Points A, B, C and D are on the circle. Point A is on the top middle, point B is on the bottom right, point C is slightly above the middle right, and point D is on the bottom left.
3. A line segment connects points A and B.
4. A line segment connects points C and D.
5. A line segment connects points A and D.
6. A line segment connects points C and B.
7. Point E is the intersection of line segments A B and C D. Point E is to the right and slightly below point O.

Given:AE = 7

EB = 4

DC = 16

Find:DE and EC

(Assume DE > EC.)

Answer 1

DE·EC = AE·EB = 7·4 = 28;

DE + EC = DC = 16; EC = 16 - DE

DE(16 - DE) = 28; DE² - 16DE + 28 = 0 ; (DE - 2)(DE - 14) = 0; DE = 14 and EC = 2