At the endpoints, x = 3 and x = -1, the series basically becomes 3 times the harmonic series, since the numerator is either 3·2n or 3·(-2)n, which cancels with the 2n in the denominator. However, since the harmonic series is only conditionally convegent (ie when the signs of the terms alternate), the series converges for x = -1 but diverges for x = 3. Thus, the interval of convergence is [ -1 , 3 ).
Bob M.
asked • 04/14/21The power series has a radius of convergence R = 2. Determine the interval of convergence.
The power series 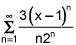 has a radius of convergence R = 2. Determine the interval of convergence.
has a radius of convergence R = 2. Determine the interval of convergence.
| (-1, 3) | |
| [-1, 3] | |
| (-1, 3] | |
| [-1, 3) |
Follow
•
1
Add comment
More
Report
1 Expert Answer
Still looking for help? Get the right answer, fast.
Ask a question for free
Get a free answer to a quick problem.
Most questions answered within 4 hours.
OR
Find an Online Tutor Now
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.





