Paul D. answered • 04/11/21
Tutor
5
(174)
PhD in Mathematics - Specializing in AP Calculus
Answer: C
- If ∑ anxn is convergent at x = −2, then the radius of convergence R ≥ 2. If R = 2, then it is still possible that the series is divergent at the endpoint x = 2. A counterexample is ∑ anxn = ∑ xn ⁄ (n2n).
- If ∑ anxn is convergent at x = −3, then the radius of convergence R ≥ 3, so x = −2 lies inside the interval of convergence and thus the series is convergent at x = −2.
- If ∑ anxn has interval of convergence (−1, 1), then the interval of convergence of ∑ an(x − 2)n is given by −1 < x - 2 < 1 or 1 < x < 3.


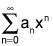 converges for x = -2, then it also converges for x = 2.
converges for x = -2, then it also converges for x = 2.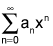 converges for x = -3, then it also converges for x = -2.
converges for x = -3, then it also converges for x = -2.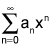 is (-1, 1), then the interval of convergence for
is (-1, 1), then the interval of convergence for 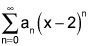 is (2, 3)
is (2, 3)

