Find the interval of convergence

Question

Find the interval of convergence for  .

	(−3, 7)
	[−3, 7)
	(−3, 7]
	[−3, 7]

Answer 1

l (a_k+1) / a_k l = [(k+1)² /5^k+1] l (x-2)l^k+1[5^k / k²] / lx-2l^k = (1/5)[(k+1)/k]² l x-2 l

As k approaches infinity, the expression above has limit l x - 2 l / 5

According to the Ratio Test, the given series converges absolutely (and therefore converges) as long as

l x - 2 l / 5 < 1.

So, l x - 2 l < 5. Thus, -5 < x - 2 < 5. We therefore have convergence if -3 < x < 7.

Checking the endpoints separately (the Ratio Test is inconclusive there):

When x = -3, the original series becomes ∑k² (diverges)

When x = 7, we get ∑(-1)^kk² = -1 + 4 - 9 + 16 - 25 + ... (this one diverges also)

Interval of convergence: -3 < x < 7.
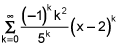