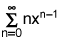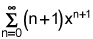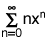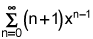Dayv O. answered • 04/07/21
Caring Super Enthusiastic Knowledgeable Calculus Tutor
it is the choice (n+1)x(n-1)
look at problem this way, let k=n-1 so if n=1 then k=0. change the sum to k=0 to infinity
to adjust the terms notice that n=k+1, substitute for all n in the term, so now have sum k=0 to infinity
of (k+1)x(k+1-2)=(k+1)x(k-1), now let n=k and the sum is from n=0 to infinity of (n+1)x(n-1).
if nervous about answer you can always check answer.
first two terms with n=1 start and nx(n-2)are 1*x-1, and 2*x0
first two terms with n=0 start and (n+1)x(n-1) are 1*x-1, and 2*x0


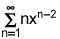 so that its lower index of summation is n = 0.
so that its lower index of summation is n = 0.