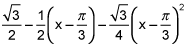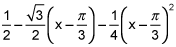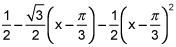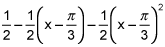Which of the following is the second order Taylor polynomial, P2(x), for f(x) = cos(x) centered at a equals pi over 3 ?

Question

Which of the following is the second order Taylor polynomial, P2(x), for f(x) = cos(x) centered at  ?

A
B
C
D

Answer 1

For a function f(x), the Taylor polynomial centered at a is

P(x) = ∑ (f⁽ⁱ⁾(a) / i!) (x-a)ⁱ

where i ranges from 0 to infinity.

For the second order Taylor polynomial, i ranges only from 0 to 2

P2(x) = f(a) + f'(a)(x-a) + (f"(a)/2)(x-a)²

The derivatives of f(x) at a = π/3:

f(x) = cos(x) f(π/3) = 1/2

f'(x) = -sin(x) f'(π/3) = -√3/2

f"(x) = -cos(x) f"(π/3) = -1/2

P2(x) = 1/2 - (√3/2)(x-π/3) - (1/4)(x-π/3)²
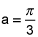