Given: ⊙O with AB ≅ AC. ∠BOC = 76° Find the following in degrees. (a) m∠ABO

Question

Consider the following figure.

Given: ⊙O with AB ≅ AC.
∠BOC = 76°

Find the following in degrees.

(a) m∠ABO

Answer 1

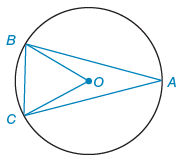
First, since the angles are located in a circle, you know that the central angle will always be exactly double the inscribed angle. Therefore, <BAC= 1/2 <BOC. Therefore, angle BAC will be 38 degrees. Since triangle ABC is isosceles, you know that <ABC=<ACB, so since the sum of <ABC+<BAC+<ACB=180 degrees, you know that <ABC= (180-38)/2=71 degrees. Similarly, since <OBC+<BOC+<OCB=180 degrees and this triangle is also isosceles since it has legs that are radii, then <OBC=<OCB, so since <BOC=76 degrees, <OBC= 52 degrees. Thus since <ABO=<ABC-<OBC, we find that <ABO is 19 degrees.