an+1 = 4n+1 / (n+1)! , an = 4n / n!
an+1 / an = [4n+1 / (n+1)! ] / [4n / n!]
= (4n+1 / (n+1)!) · (n! / 4n)
= 4 / (n+1)
limn→∞ [4 / (n+1)] = 0 so the series converges.
Nic C.
asked • 03/31/21 Use the ratio test to show that the series 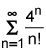 is convergent. Be sure to show your work.
is convergent. Be sure to show your work.
an+1 = 4n+1 / (n+1)! , an = 4n / n!
an+1 / an = [4n+1 / (n+1)! ] / [4n / n!]
= (4n+1 / (n+1)!) · (n! / 4n)
= 4 / (n+1)
limn→∞ [4 / (n+1)] = 0 so the series converges.
Get a free answer to a quick problem.
Most questions answered within 4 hours.
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.