Tom K. answered • 03/27/21
Knowledgeable and Friendly Math and Statistics Tutor
To show that it is convergent by the alternating series test, we note that the sign of the sequence of terms alternates and 3/n^2 converges monotonically to 0.
With such series, the error is less than the absolute value of the next term.
Thus, for an error less than .05, we set 3/n^2 = .05
n^2 = 60
n = 7.75
As the absolute value of the term for n = 8 is less than .05, n = 7
It turns out that using the next term overestimates the number of terms required. 5 is sufficient.


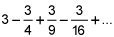 is convergent by the alternating series test, and find the number of terms necessary to estimate the sum of the series with an error of less than 0.05.
is convergent by the alternating series test, and find the number of terms necessary to estimate the sum of the series with an error of less than 0.05.

