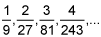Determine the nth term formula for each of the following sequences and find the limit if it exists

Question

Determine the nth term formula for each of the following sequences and find the limit if it exists.

1. 
2. -3, 3,-3, 3, …

Answer 1

The general term is n(1/3)^n+1.

The sum is 1+r∑nrⁿ where r=1/3 and the sum runs from1 to ∞

If you write this sum as follow

r

r²+r²

r³+r³+r³

and so forth, you will show that sum can be written as a double sum 1+r∑∑r^k, where again r=1/3 and the righthand sum runs from k=n to ∞ and the lefthand sum runs from 1 to ∞.

Since both the sums are geometric series the sums evaluate to 1+[r/(1-r)]² which is 5/4 when you plug in the value for r.

There is another way to arrive at the formula for the sum using finite differences and summation by parts. If

you want to see that derivation, make a comment & I will try to get it to you.