Tom K. answered • 03/24/21
Knowledgeable and Friendly Math and Statistics Tutor
The obvious answer is D, as the alternating nature of the sum guarantees that the error is less than the next term.
A more sophisticated analysis would show that 5000 is sufficient. That is because we can rewrite the remainder, up to a sign as 1/(n+1)(n+2) + 1/(n+3)(n+4) + ...which is less than 1/2 the integral of 1/k^2 from k = n to infinity = 1/2n


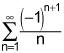 is convergent, find a value of n for which the nth partial sum is guaranteed to approximate the sum of the series with an error of less than 0.0001
is convergent, find a value of n for which the nth partial sum is guaranteed to approximate the sum of the series with an error of less than 0.0001

