I will explain for you here that we can use integral test
suppose f is a continuous , positive and decreasing on the interval [ 1, ∞) , and let an = f (n) . Then the series
∞
∑ an is convergent if and only if the improper integral
n=1
∞
∫ f(x) dx is convergent.
1
Since 1/ (n+1 )2 < 1 / n 2 the series is decreasing, or you can prove that by taking the first derivative for f(n) and you will find it negative]
Now
∞ t ∞
∫ 1/x2 dx = lim ∫ 1/x2 dx = lim -1/x ⌉ = - lim [ 1/t - 1] = 1 convergent
1 t→∞ 1 t → ∞ 1 t → ∞
Hence
∞
∑ 1/ n2 is convergent by the integral test.
n=1


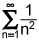 is convergent.
is convergent. 


