Which of the following statements is true for the series the summation from n equals 1 to infinity of the quotient of the sine of n and 2 to the nth power ?

Question

Which of the following statements is true for the series  ?

A	The alternating test applies but is inconclusive.
B	The series converges conditionally.
C	The series diverges.
D	The series converges absolutely.

Answer 1

We see that sin(n) will alternate in sign as n increases from 1 to infinity (although not aligned to points of π/2, we do know that sin(x) will oscillate between values of -1 and 1.

So to remove the alternating aspect, provide an upper bound for the sin(n)/2ⁿ ≤ |sin(n)|/2ⁿ ≤ 1/2ⁿ

Taking the infinite sum (lower bound = 1, upper bound = infinity) we can find the sum of 1/2ⁿ over this range of n as 1. Since the non-alternating sum is bounded, the alternating series in this case, is also bounded to be less than or equal to 1. This proves the original summation is bounded and is less than 1 (convergence). Furthermore, since the non-alternating series converges on its own, the alternating sum also converges (absolutely).

So we have absolute convergence (D)
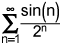