For similar triangles corresponding sides are in proportion so:
CD/CB = CE/CA
Since CD = 10 and CA = 12 and CB = CE + EB and EB = 14:
10/(CE + 14) = CE/12
cross-multiplying:
CE^2 + 14CE = 120
CE^2 +14CE - 120 = 0
(CE + 20)(CE - 6) = 0
CE = 6
Alyssa Z.
asked • 03/20/21△CDE ~ △CBA with ∠CDE ≅ ∠B.
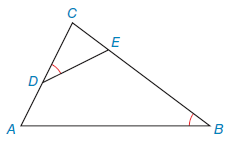
If CD = 10, CA = 12, and EB = 14, find CE.
For similar triangles corresponding sides are in proportion so:
CD/CB = CE/CA
Since CD = 10 and CA = 12 and CB = CE + EB and EB = 14:
10/(CE + 14) = CE/12
cross-multiplying:
CE^2 + 14CE = 120
CE^2 +14CE - 120 = 0
(CE + 20)(CE - 6) = 0
CE = 6
Get a free answer to a quick problem.
Most questions answered within 4 hours.
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.