Michael K. answered • 03/11/21
PhD professional for Math, Physics, and CS Tutoring and Martial Arts
Using the alternating series convergence test which is nothing more than understanding the if the absolute value of the summation would also converge gives us three possibilities...
- absolute value of terms converge in sum --> alternating series converges absolutely
- absolute value of terms diverge in sum --> possible conditional converge of alternating series
- diverge of alternating series --> divergence
In A. the abs value of each term is 1/n^2 which is know to converge by the p-series test. So we have absolute converge of the alternating series.
In B, the absolute value would diverge, the alternating series depends on how the grouping of -1, 1 is done and could give a result of 1, -1, 0. Since it oscillates it would be considered an divergent series.
In C, looking at the absolute value of n/(n+1) the limit approaches 1 in the ratio-test which states that it is divergent. In this case we have the sum (first few terms...)
1/2, -2/3, +4/5, -5/6, 6/7, ...
This series diverges even with the alternating signs due to the jumping from -1, 1 (very much like the answer in B
In D, we have the absolute value of 1/sqrt(n) or n^{-1/2} which is a divergence series. The alternating aspect does not assist with convergence much as the argument posed in C (when using the ratio limit test)



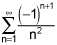
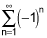
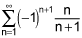
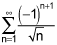



Michael K.
03/11/21