Michael K. answered • 03/11/21
PhD professional for Math, Physics, and CS Tutoring and Martial Arts
This problem is interesting in that we have two competing "large" functions 2^n and n!. The question is if we look at the ratio test (ignoring the alternating series component) is the summation converge? The answer is yes and here is why...
2^n is nothing more than a collection of 2's multiplies together. n! is a sequence of integers multiplied together. Let's compare these two series...
lets say n = 1: 2^1 = 2, n! = 1. (this would no survive the ratio series test
lets say n = 2 : 2^2 = 4, n! = 2
...
lets day n = 4 : 2^4 = 16, n! = 24 (1 * 2 * 3 * 4 ) > 2 * 2 * 2 * 2
So as n increases n! grows faster than 2^n and that can be seen if you use the approximation for n! using Sterling's approximation (which states n! ~ e^n). since e^n > 2^n for all n, this limit 2^n/n! approaches zero in the limit as n-> infinity.
Since we have an absolutely convergent series in the non-alternating series sum, if we add the alternating series component we still have converge.
So this series will absolute converge!


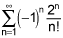




Marya H.
can you help with my question?03/11/21