(a) m∠P in degrees, if m∠MNP − m∠P = 58° B. (b)the length of side NP (in cm), if MN = 14 cm, MQ = 15 cm, and PQ = 22 cm

Question

With MN ∥ QP and ∠M ≅ ∠Q, MNPQ is a right trapezoid. Find the following.

(a) m∠P in degrees, if m∠MNP − m∠P = 58°

B. (b)the length of side NP (in cm), if MN = 14 cm, MQ = 15 cm, and PQ = 22 cm

Answer 1

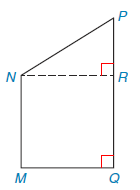
a)

NR is parallel to MQ because <NRP and <MQR are equal corresponding angles, so that MNRQ is a parallelogram. Because consecutive angles of a parallelogram are supplementary, MNRQ is a rectangle.

Because PNR is a right triangle, <RNP and <P are complementary, ie., m<RNP + m<P = 90, so

m<RNP = 90 - m<P

m<MNR + m<RNP = m<MNP

m<MNR = 90 so

90 + m<RNP = m<MNP

since m<RNP = 90 = m<P and m<MNP = 58 + m<P:

90 + 90 - m<P = 58 + m<P

solve for m<P:

122 = 2m<P

m<P = 61

b)

QR = MN = 14 because opposite sides of a parallelogram are equal

NR = MQ = 15 for the same reason

Since PQ = 22 and QR = 14, then PR = 22-14 = 8

By the Pythagorean Theorem: NP, the hypotenuse is sqrt(8^2 + 15^2) = 17