x=2 cos θ + cos2θ
y=2 sin θ + sin θ cos θ
dx/dθ = 2 sin θ (1+cos θ)
dy/dt = 2cos θ + cos 2θ
dy/dx = (dy/dt)/(dx/dt) ....you can write that out for yourself
At π/2
x=0, y=2 and dy/dx = 1/2
The tangent is 1/2 = (y-2)/x, i.e. y = (x/2)+2.
I graphed it on my graphing utility and it looked pretty good!
P.S.
I never did this before...so tutors learn things too!
P.P.S.
Just in case you should need it, the polar form of the tangent line is:
r=2/(sin θ-.5 cos θ)


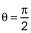 . You must show your work.
. You must show your work.


