
Brandon B. answered • 03/02/21
Physics PhD. 10+ years teaching calculus based physics.
Arc length is ∫ds = ∫(dx2+dy2)1/2 = ∫(1 + dy2/dx2)1/2 dx. So we see that dy/dx = cosx ⇒ y = sinx + C. y(0) = 0 ⇒ C = 0.
Cameron L.
asked • 03/02/21Find the equation of the curve that passes through the point (x, y) = (0, 0) and has an arc length on the interval 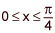 given by the integral
given by the integral 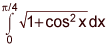
| A | y = sin(x) |
| B | y = cos(x) |
| C | y = cos-1(x) |
| D | y = tan(x) |

Brandon B. answered • 03/02/21
Physics PhD. 10+ years teaching calculus based physics.
Arc length is ∫ds = ∫(dx2+dy2)1/2 = ∫(1 + dy2/dx2)1/2 dx. So we see that dy/dx = cosx ⇒ y = sinx + C. y(0) = 0 ⇒ C = 0.
Get a free answer to a quick problem.
Most questions answered within 4 hours.
Choose an expert and meet online. No packages or subscriptions, pay only for the time you need.