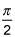Bradford T. answered • 03/01/21
Retired Engineer / Upper level math instructor
x = rcos(θ)
y = rsin(θ)
dy = r'sin(θ) + rcos(θ)
dx = r'cos(θ) -rsin(θ)
dy/dx = (r'sin(θ) + rcos(θ))/( r'cos(θ) -rsin(θ))
r = 1+2sin(θ)
r' = 2cos(θ)
dy/dx = (2cos(θ)sin(θ)+(1+2sin(θ))cos(θ))/(2cos(θ)cos(θ) -(1+2sin(θ))sin(θ))
at θ=π/2
y'(π/2) = (0+0)/(0-(3)(1)) = 0 Answer D
If you plot 1-2sin(θ), at θ= π/2, you have two y-intercepts at y=1 and y=3 which are tangent lines with slope = 0.


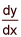 of the polar curve r = 1 + 2 sin θ at θ =
of the polar curve r = 1 + 2 sin θ at θ =