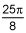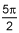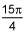John L. answered • 02/25/21
Naval Academy graduate with more than 10 years experience in teaching
The answers listed for this problem are incorrect. The correct answer is 25pi/4. Here's why. For the polar curve listed, the first pedal would be achieved with the bounds from 0-pi/2 (keep in mind that when a function is f(cx), it is compressed by a factor of c (c>0). So the normal period for the first hump of the sin(x) would be from 0 to pi, halving that gets to pi/2.
The area of a polar curve A = integral R^2 d-theta. Here, R^2 = 25sin^2(2theta). There is a trig substitution formula which states sin^2(x) = (1-cos(2x))/2 so sin^(2x) = (1 - cos(4x))/2
So we integrate from 0-pi/2 25/2 IntegralSign [1-cos(4theta)] dtheta which yields 25/2 * [theta - 0.25(sin(theta)] evaluated from 0-pi/2.
Plug pi/2 into formula yields pi/2. Plug 0 into formula gets 0. By Fundamental theory of calc part 2, the difference is the area or 25pi/4