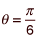Find the slope of the tangent line to the polar curve r = 2 sin θ at the point where theta equals pi over 6

Question

Find the slope of the tangent line to the polar curve r = 2 sin θ at the point where 

A	0
B	1
C	-1
D	None of these

Answer 1

Since r is a function of θ and r² =x² + y² we can determine x'(θ) and y'(θ) to determine dy/dx

r = 2sinθ so x = r cos θ = 2 sin θ cos θ and y = r sin θ = 2 sin² θ

x'(θ) = 2 cos² θ - 2 sin² θ = 2 cos (2θ) and y'(θ) = 4 sin θ cos θ = 2 sin (2θ)

dy/dx = y'(θ)/x'(θ) = 2 sin (2θ)/ 2 cos (2θ) = tan (2θ)

Since you are finding the slope when θ = π/6, dy/dx = tan (2π/6) = tan (π/3) = √3

Answer 2

Slope m of tangent line is m = dy/dx;

x = rcosθ = 2sinθcosθ = sin2θ;

y = rsinθ= 2sin²θ = 1 - cos2θ

θ = π/6; x = sinπ/3 = √3/2; y = 1 - cosπ/3 = 1/2

dy/dx = (dy/dθ)/(dx/dθ) = 2sin2θ/2cos2θ = tan2θ = tanπ/3 = √3

Answer is D